如何預(yù)測直接數(shù)字頻率合成器(DDS)輸出頻譜中主相位截?cái)嚯s散的頻率和幅度
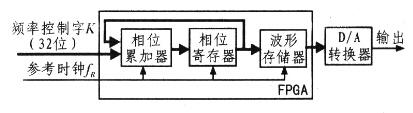
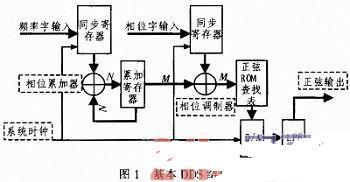
現(xiàn)代直接數(shù)字頻率合成器(DDS)通常利用累加器和數(shù)字頻率調(diào)諧字(FTW)在累加器輸出端產(chǎn)生周期性的N位數(shù)字斜坡(見圖1)。 此數(shù)字斜坡可依據(jù)公式1定義DDS的輸出頻率(fO),其中fS為DDS采樣速率(或系統(tǒng)時鐘頻率)。
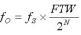 (1)
(1)DDS給定時,組成FTW的位數(shù)(N)定義了fO的最小可能變化,這發(fā)生在FTW值僅更改最低有效位(LSB)時。 也就是說,F(xiàn)TW中的1 LSB變化定義了DDS的調(diào)諧分辨率。 例如,N = 32的DDS的調(diào)諧分辨率高于N = 24的DDS。為了證實(shí)DDS的極佳調(diào)諧能力,以AD9912為例,N = 48產(chǎn)生的調(diào)諧分辨率為1/248(即1/281,474,976,710,656)。 事實(shí)上,fS = 1 GHz時,AD9912產(chǎn)生的頻率調(diào)諧分辨率約為3.6 µHz (0.0000036 Hz)。
若DDS的FTW為N位,細(xì)看圖1可知,累加器輸出端的位數(shù)(N)和角度轉(zhuǎn)幅度模塊輸入端的位數(shù)(P)之間存在明顯的差異,即P ≤ N。這種差異會導(dǎo)致DDS輸出頻譜中出現(xiàn)相位截?cái)嚯s散。
知道給定DDS的P值對預(yù)測相位截?cái)嚯s散非常重要。 本應(yīng)用筆記介紹了一種用于計(jì)算特定相位截?cái)嚯s散的頻率和幅度的方法,尤其適合給定FTW的主相位截?cái)?PPT)。
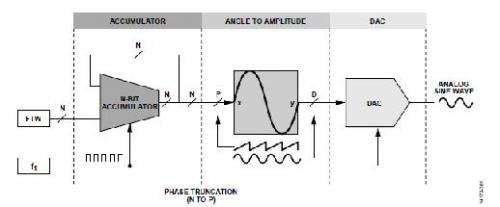
圖1. DDS功能框圖
相位截?cái)?/strong>
累加器和FTW組成DDS的頻率控制元件。 但是,除了頻率控制元件外,DDS還具有將N位累加器輸出從相位值轉(zhuǎn)換為幅度值的角度轉(zhuǎn)幅度模塊。 角度轉(zhuǎn)幅度模塊占據(jù)了DDS數(shù)字電路的很大一部分。 因此,通過增大N來提高DDS的調(diào)諧分辨率會大幅增加角度轉(zhuǎn)幅度模塊所需的電路數(shù)。 同樣,將所有N位相位信息轉(zhuǎn)換為幅度不太實(shí)際。 如圖1所示,實(shí)際DDS使用累加器位的子集進(jìn)行相位幅度轉(zhuǎn)換,即P最高有效位(MSB)。 這種位截?cái)鄷蠓鶞p少角度轉(zhuǎn)幅度模塊所需的電路數(shù)。 但代價是需要在DDS輸出端引入可能的頻譜偽像(具體而言就是相位截?cái)嚯s散)。
相位截?cái)嚯s散
根據(jù)定義,按P = N設(shè)計(jì)的DDS沒有相位截?cái)唷?因此,其輸出頻譜中沒有相位截?cái)嚯s散。 但是在實(shí)際DDS中,P N,這會產(chǎn)生相位截?cái)唷?/div>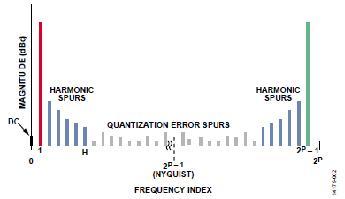

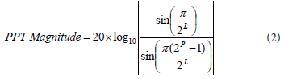

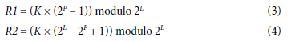




有三類相位截?cái)嚯s散: 一階、二階和三階。 這幾個分類源于DDS中相位幅度轉(zhuǎn)換器和數(shù)模轉(zhuǎn)換器(DAC)的級聯(lián)組合的頻譜特性。 圖2結(jié)合圖形說明將傅里葉變換技術(shù)應(yīng)用于角度轉(zhuǎn)幅度模塊(帶P位相位輸入)和呈現(xiàn)諧波失真的非理想DAC所產(chǎn)生的譜線。 一般而言,頻譜由2P個頻率構(gòu)成,指數(shù)范圍為0至2P − 1,分類詳情如表1。

圖2. 角度轉(zhuǎn)幅度模塊和DAC的頻譜特性
主相位截?cái)?PPT)雜散
每階(一階、二階和三階)的許多相位截?cái)嚯s散可能在DDS的輸出頻譜中出現(xiàn),具體取決于FTW的特定值。 本應(yīng)用筆記重點(diǎn)介紹最大的一階雜散,即PPT雜散。
由于DDS輸出是從相位采樣生成波形的結(jié)果(即累加器輸出),因此DDS輸出頻譜遵循奈奎斯特采樣理論的規(guī)則。 輸出頻譜顯示為兩個完全相同的頻譜,每個頻譜跨越采樣頻率(fS)一半的頻率范圍。 這兩個頻譜是彼此的鏡像,反映奈奎斯特頻率(fS/2)。 同樣,PPT雜散將其自身表示為兩個雜散。 一個PPT雜散出現(xiàn)在0 Hz和fS/2之間,另一個作為其鏡像出現(xiàn)在fS/2和fS之間。
請注意,盡管兩個PPT雜散是最大的一階相位截?cái)嚯s散,但整體而言,這些雜散可能不是最大的相位截?cái)嚯s散。 由于相位截?cái)嚯s散在DDS輸出頻譜中的分配機(jī)制,部分二階相位截?cái)嚯s散的幅度可能大于PPT雜散。
我們無法預(yù)測二階或三階相位截?cái)嚯s散的幅度。 二階相位截?cái)嚯s散幅度取決于DAC的諧波失真特性,這些特性因器件而異。 三階相位截?cái)嚯s散幅度與量化誤差相關(guān),而量化誤差基本上是隨機(jī)的。

表1. 圖2中顯示的頻率分類
最右側(cè)的非零位
計(jì)算PPT雜散的幅度和頻率位置需要知道以下參數(shù):
•DDS采樣速率(fS)
•兩個DDS參數(shù):N和P
•FTW的特定值
對于給定應(yīng)用,N和P固定,fS通常為恒定值。 相反,F(xiàn)TW完全可變,控制fO的值(詳見公式1)。FTW的值不僅控制DDS輸出頻譜中fO的位置,而且控制相位截?cái)嚯s散的位置。 事實(shí)上,對于DDS輸出頻譜,給定FTW的最重要特性是以二進(jìn)制形式表示時的尾隨零數(shù)量。 尾隨零數(shù)量定義了重要參數(shù)L,即FTW最右側(cè)非零位的位置。
FTW中的L位位置取決于FTW的特定值(切記,F(xiàn)TW的值依據(jù)所需DDS輸出頻率而變化,詳見公式1)。 這種依賴性非常大,因?yàn)槿我饨o定FTW的L位位置決定相位截?cái)嚯s散在DDS輸出頻譜中的分配方式。
對于任意給定FTW,圖3演示了如何找到L的值。首先,將FTW轉(zhuǎn)換為二進(jìn)制。 然后,將指數(shù)值分配給FTW位,MSB的起始指數(shù)值為1。圖3為一個32位FTW的示例;因此,指數(shù)范圍為1至32。L值是值為1的最后一位的指數(shù)(從MSB向LSB讀)。 圖3中的FTW值為0x0036e580(十六進(jìn)制),因此,采用本協(xié)議時,此特定FTW的L的值為25。
給定FTW的L的值最為重要。 首先,L決定相位截?cái)嚯s散是否出現(xiàn)在DDS輸出頻譜中。 若L ≤ P,則沒有相位截?cái)嚯s散。 若L > P,則包括PPT雜散在內(nèi)的相位截?cái)嚯s散出現(xiàn)在DDS輸出頻譜中。 其次,L和P的值可確定PPT雜散的幅度和頻率(假定L > P)。
PPT幅度
兩個PPT雜散具有相同的幅度(見公式2)。 若已知特定FTW的值和給定DDS設(shè)計(jì)的P值,兩個PPT雜散的幅度為:
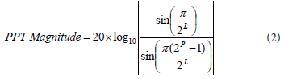

其中,PPT幅度的值以dBc為單位: 與頻率為fO時主DDS輸出信號的幅度相關(guān)的分貝。
請注意,公式2中的兩個正弦函數(shù)的參數(shù)以弧度為單位。 例如,假設(shè)DDS的P = 19,F(xiàn)TW如圖3所示,則使用公式2得到的PPT雜散幅度為−114.38789 dBc。
PPT頻率
需要多個步驟才能確定這兩個PPT頻率。 第一步,得出K的值,F(xiàn)TW的十進(jìn)制值截?cái)酁長位。 要得到K,在FTW為二進(jìn)制形式的情況下,消除尾隨0并將得到的L位FTW轉(zhuǎn)換為相應(yīng)的十進(jìn)制值。 例如,圖3中的FTW可得到K = 28,107(通過將二進(jìn)制數(shù)字0000000000110110111001011轉(zhuǎn)換為相應(yīng)的十進(jìn)制數(shù)字得出)。
使用K計(jì)算兩個PPT雜散的頻譜指數(shù)位置(R1和R2),如下面的公式3和公式4所示:
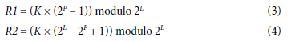

例如,在DDS的P = 19且FTW如圖3所示的情況下,公式3中括號內(nèi)的數(shù)字為14,736,134,709,公式4中括號內(nèi)的數(shù)字為928,378,285,515。將225模數(shù)應(yīng)用于這些值可得到
R1 = 5,739,061
R2 = 27,815,371
根據(jù)下面的公式5和公式6,使用R1和R2確定DDS輸出頻譜中的兩個PPT頻率位置(fPPT1和fPPT2)。

例如,若fS = 250 MHz,F(xiàn)TW如圖3所示,且R1和R2的值已在前面的例子中計(jì)算出,則兩個PPT雜散頻率如下:


結(jié)論
盡管本應(yīng)用筆記介紹了一種相對簡單的方式來預(yù)測兩個PPT雜散的頻率和幅度,但公式3和公式4可能引起計(jì)算問題。 具體而言,括號內(nèi)的數(shù)字由一個整數(shù)定義,可能非常大。
為了解釋這些計(jì)算中較大整數(shù)引起的問題,試重新考慮AD9912,其中N = 48,P = 19。假定FTW為0x400000000001(十六進(jìn)制),即70,368,744,177,665(十進(jìn)制)。 在此例中,L = 48;因此,K的值與FTW相同。
現(xiàn)在考慮公式4中括號內(nèi)的數(shù)字。2L – 2P + 1可得到以下值:
248 – 219 + 1 = 281,474,976,186,369
因此,由公式4中括號內(nèi)的數(shù)字可得到
K × (2L – 2P + 1) = 70,368,744,177,665 × 281,474,976,186,369 = 19,807,040,591,672,948,094,687,248,385
以二進(jìn)制形式表示此整數(shù)需要94位。 大部分計(jì)算軟件工具無法精確表示這種大小的整數(shù)。 例如,在64位機(jī)器上運(yùn)行的MATLAB將K × (2L – 2P + 1)表示為浮點(diǎn)數(shù):1.980704059167295 × 1028。對應(yīng)的整數(shù)為19,807,040,591,672,950,000,000,000,000。此值與真實(shí)值偏差較大,因此得到的R2并不正確。
事實(shí)上,不僅大部分軟件工具無法處理極大整數(shù),而且大部分計(jì)算機(jī)內(nèi)部的處理器芯片也無法處理極大整數(shù)。 例如,一臺帶64位處理器的計(jì)算機(jī)無法處理94位整數(shù)。 這個問題至關(guān)重要,因?yàn)橛?jì)算R1和R2值需要極大整數(shù)計(jì)算,這超出了大部分計(jì)算機(jī)的能力。
除了正確表示公式3和公式4中括號內(nèi)的數(shù)字,還需要計(jì)算括號內(nèi)數(shù)字的2L模數(shù)。 在前面的例子中,L = 48,這意味著模數(shù)達(dá)48位。 大部分計(jì)算機(jī)不支持超過32位的模數(shù)計(jì)算。
總而言之,公式3和公式4產(chǎn)生的難題在使用軟件工具實(shí)現(xiàn)PPT雜散計(jì)算時需要特別注意。 用戶必須將括號內(nèi)的數(shù)字作為一個整數(shù)進(jìn)行正確計(jì)算(無截?cái)嗷蛩纳嵛迦耄?,并且?yīng)在不損失精度的情況下正確處理模數(shù)計(jì)算。
盡管大部分軟件工具和處理器無法直接處理極大整數(shù),但也有例外。 例如,軟件工具Python本身支持極大整數(shù)計(jì)算。 盡管MATLAB®本身無法處理極大整數(shù),但支持極大整數(shù)計(jì)算的可變精度整數(shù)(VPI)工具箱可在MATLAB Central的Math Works網(wǎng)站上免費(fèi)下載。
關(guān)鍵詞:
直接數(shù)字頻率合成器
DDS
FTW
相關(guān)推薦
技術(shù)專區(qū)
- FPGA
- DSP
- MCU
- 示波器
- 步進(jìn)電機(jī)
- Zigbee
- LabVIEW
- Arduino
- RFID
- NFC
- STM32
- Protel
- GPS
- MSP430
- Multisim
- 濾波器
- CAN總線
- 開關(guān)電源
- 單片機(jī)
- PCB
- USB
- ARM
- CPLD
- 連接器
- MEMS
- CMOS
- MIPS
- EMC
- EDA
- ROM
- 陀螺儀
- VHDL
- 比較器
- Verilog
- 穩(wěn)壓電源
- RAM
- AVR
- 傳感器
- 可控硅
- IGBT
- 嵌入式開發(fā)
- 逆變器
- Quartus
- RS-232
- Cyclone
- 電位器
- 電機(jī)控制
- 藍(lán)牙
- PLC
- PWM
- 汽車電子
- 轉(zhuǎn)換器
- 電源管理
- 信號放大器





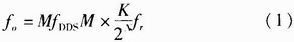

評論